https://patents.google.com/patent/WO2019080933A1/zh

摘要

问题

  1. 解决交易信息透明，造成隐私信息暴露
  2. 论文提出解决方案使用到了秘密共享方式，解决共谋问题
  3. 确保关键字安全性

预处理方法

  1. 将层次属性加密与线性秘密共享相结合，提出了一种基于可搜索属性加密的区块链数据隐私保护控制方案，解决了传统区块链交易中的隐私暴露问题。
  2. 用户的访问控制由验证节点实现，避免了向区块链网络提交私钥和访问结构的安全风险。将私钥组件与区块链中用户节点的随机身份相关联可以解决共谋问题
  3. 授权用户可以通过可搜索的加密来快速搜索和监督交易信息。改进的算法确保了关键字的安全性。【算法应该看不懂】

背景

  1. 提出基于椭圆曲线加密算法m的更有效的盲签名混合方案—该方案简单易用，通常适用于各种数字货币，【但它是集中式货币方案】。

    传统公钥密码体制（密钥长度一般为512bit）随着计算机运算速度的提升，已经有被破解的趋势了，同时RSA运算效率较低。利用曲线上的有理点组成的Abel群《TODO》及其上离散对数问题求解的困难性构成一些公钥密码体制，即密钥的每个bit都具有最高的安全强度，椭圆曲线密码体制中160bit长的密钥所展示的安全强度相当于RSA的1024bit

  2. 使用盲签名之类《TODO》的混合加密技术—区块链隐私保护机制【增加了技术成本，并且第三方实施令牌处理不可避免地增加了额外的服务开销】

  3. 提出了一种改进的基于环的秘密交易方案《TODO》

    在该方案中，大量的环签名被放置在可链接的自发匿名组签名的多层中，其解决方案可以保护身份隐私和交易隐私。尽管环签名提供了强大的匿名性，但它具有三个限制：产生交易数据较多，需要更多的记录的存储空间、签名的大小与参与者数量成正比，因此传统每个事务做了限制，每个事务有四个输出、隐藏的数量增加了检查的难度，即，它不仅验证交易期间是否生成了秘密加密货币，而且还确定了特定时刻的额外数量。

初步知识

Bilinear Mapping

双线性映射

群

  1. 封闭性——如果a和b都属于G，则a+b也属于G。
  2. 结合律——对于G中的任意元素a、b和c，都有（a+b）+c=a+（b+c）成立。
  3. 单位元——G中存在元素e，对于G中任意元素a，都有a+e=e+a=a成立。
  4. 逆元——对于G中任意元素a，G中都存在元素a’，使得a+a’=a’+a=e成立。G就叫作一个群，记为（G，+）
  5. 在群中定义求幂运算为重复使用群中的运算，如a^4 =a+a+a+a。规定a^0 =e为单位元。如果一个群的所有元素都是a的幂a^k，则称这个群是一个==循环群 #00BCD4==，这里的k是整数。a也被称为这个群的生成元。

双线性映射

设G1、G2都是阶为p的循环群，p是素数。如果映射e: G1 × G1 → G2 满足以下性质：

  1. 双线性性。
    对于任意a，b∈Zp和R，S∈G1，有e(Ra, Sb) = e(R, S)ab；
  2. 非退化性。
    存在R，S∈G1，使得e(R, S) ≠ 1G2。这里1G2代表G2群的单位元；
  3. 可计算性。
    存在有效的算法对任意的R，S∈G1，计算e(R, S)的值。
    那么称e是一个双线性映射。

Determining the Bilinear Diffie–

ellman Assumption (DBDH)

确定双线性参数生产区的假设（DBDH）

选择一个G1的生成器，设a,b,c,r属于（1，q-1）中任意质数，当g^a,g^b,g^c,g^r属于G1，e(g,g)abc和e(g,g)r属于G2,判断e(g,g)abc和e(g,g)r是否相等

判断条件：
对于任意多项式概率时间算法的对手A，解决决策双线性Diffie-Hellman（DBDH）假设[i]的优势定义为

DBDH判断条件

如果确定的值AdvDBDH A可忽略不计，则将建立决策双线性Diffie-Hellman假设。

Lsss Linear Secret Sharing Scheme

Lsss线性秘密共享方案【是对密钥的管理策略】

有趣的栗子

在信息系统中使用的秘密共享，可以防止系统密钥的遗失、损坏和来自地方的攻击，减小秘密保存者的责任。在(t,n)秘密共享体制中，秘密分发者将一个秘密信息分成n个秘密份额，分发给n 个人，当需要恢复秘密信息时，任意少于t个的秘密保存者都得不到该秘密的任何信息。
现目前进行秘密共享的主流方案有基于访问控制树和秘密共享矩阵的。基于访问控制树进行秘密分享时，通过门限控制进行合理的多项式构造，最终将秘密分享给树的每一个子节点。

模型

系统模型

基于可搜索属性加密的区块链数据隐私访问控制系统模型如图

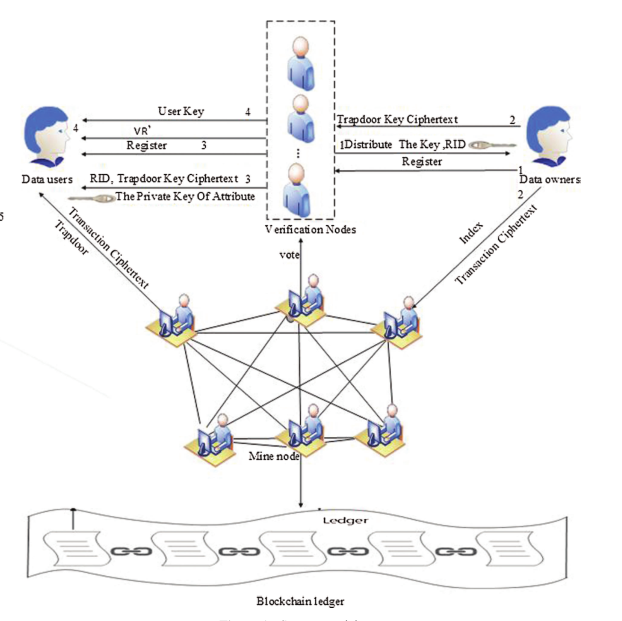
基于可搜索属性加密的区块链数据隐私访问控制系统模型

包含的四个实体

四个实体

  1. 数据所有者：首先进行初始化，生成索引密钥和陷门密钥，提取交易的关键词，然后使用索引密钥对索引进行加密，形成索引密文；其次，对陷门密钥进行加密以形成陷门密钥密文并共享数据。最后，使用安全签名算法对交易进行签名并加密，同时，数据所有者将索引关键字附加到交易密文的密文文件中。最重要的是，数据所有者可以是区块链上进行比特币交易的用户或矿工。
  2. 用户：注册系统生成与真实身份相对应的身份标识符RID和与用户属性相对应的私钥。另外，用户解密陷门密文并使用 用户密钥以生成陷门，然后发送区块链以请求交易密文。
  3. 验证节点：验证用户身份和权限的正确性，并在属性集合中计算用户的属性和私钥参数以及权限参数，以分发陷密钥密文，并将用户密钥UK分发给合法用户。
  4. 矿工节点：矿工节点在此期间广播所有交易信息，每个节点执行验证并在验证后加入区块链。计算并匹配数据所有者发送的陷门和索引，然后在匹配成功后将交易密文发送到数据使用方。

威胁模式

前提： 只有“验证节点”是完全可信的，私钥能正常生成和分发给用户。大多数矿工节点半诚实【不破坏协议，根据规则可以推测用户信息】。此外，用户可能会合谋解密他们无法访问的数据。

安全模型

安全模型是指对手与挑战者之间的博弈。

  1. IND-CPA security model【Indistinguishability under chosen-plaintext attack】

选择明文攻击。可理解为攻击者拥有加密机的使用权限，可以加密自己想加密的任何明文。攻击目的：由明文和对应的密文来分析和推断加密算法的信息，主要是加密密钥。

  • 初始化：挑战者A使用初始化算法生成公共参数和主密钥【重复使用的密钥，对称密钥】，并将主密钥发送给对手C。—-每次通信只使用一次的密钥称为会话密钥（session key）。相对于会话密钥，重复使用的密钥称为主密钥（master key）。
  • 第一步：对手C重复尝试一组属性S1-Sq，但是没有属性满足访问
  • 挑战：对手C选择两条消息M0; M1并将它们发送给挑战者A。挑战者A选择0或者1，和加密的访问结构的消息M，并将密文发送给对手C
  • 第二步：
  1. IND-CKA security model

关键字攻击

具体结构即功能实现

注册

用户向系统提交注册申请，获取真实身份信息对应的身份RID和用户属性集，数据所有者（交易用户）进行注册获取密钥和身份标识。

初始化

双线性

  1. 数据拥有者:：选择一个以质数为序的群G0,用元素g(单位元)生成群，在限制字段中选择N个元素(N为阶)，并使用系统属性形成系统属性集S，并根据属性之间的相关性来确定S中的属性。S被分为x个树，Hi被设置为i个树的深度，H为树中最大深度；随机选择向量U=(Uy)1=<x=<y和U’=(U’y’)1=<x‘=<y’，uy代表与y属性树相对应的public参数，数据所有者选择素数p的序列，并生成群G1,H1。数据拥有者选择两个随机数η(姨塔)，μ(谬)，然后计算生成公钥PK={g,gμ}和私钥SK=η代表陷门。
  2. 验证结点：Z*p在有限域中用p-基元表达一组元素，从中选择两个大小不同的随机数α，β，验证结点通过计算PK={G0,g,gβ,Y=e(g,g)α,U,U’}和MK={α，β}来定义一个双线性图e:G0xG0=G1。
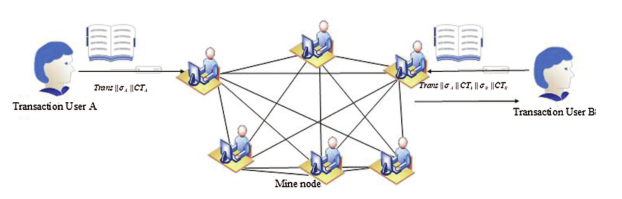
  3. 交易生成和签名：交易用户A生成交易信息，通过钱包签名算法对自身身份进行加密，并使用钱包地址对应的私钥对其签名，然后发送给交易用户B。签名的算法如下()：

签名算法

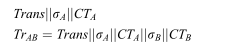
Trans:交易信息、
δ A为用户自身加密后的信息即用于标识、
CTA（Ciphertext密文）私钥加密产生签名

  1. 产生索引：交易者从交易明文信息中提取关键字，并用索引密钥gμ和两个随机数字进行加密。
  2. 加密：Encrypt(M，TK，PK)[信息，非对称传输密钥，公钥]