kernal
定义
核方法是一类把低维空间的非线性可分问题,转化为高维空间的线性可分问题的方法。
理论基础:核方法的理论基础是Cover’s theorem,指的是对于非线性可分的训练集,可以大概率通过将其非线性映射到一个高维空间来转化成线性可分的训练集。
核函数是映射关系 的内积,映射函数本身仅仅是一种映射关系,并没有增加维度的特性,不过可以利用核函数的特性,构造可以增加维度的核函数。
设 是输入空间(即 , 是 的子集或离散集合 ),又设 为特征空间( 是希尔伯特空间),如果存在一个从 到 的映射
使得对所有 ,函数满足条件
则称 $K$ 为核函数。其中 为映射函数, 为内积。
即核函数输入两个向量,它返回的值等于这两个向量分别作 映射然后点积【内积】的结果。
核技巧是一种利用核函数直接计算 ,以避开分别计算 和 ,从而加速核方法计算的技巧。
注意
得益于SVM对偶问题的表现形式,核技巧可以应用于SVM。
TODO 没有了解
核函数的选择是SVM的最大变数,如果核函数选择不适,那么 将不能将输入空间映射到线性可分的特征空间。
判断核函数
不知道 的情况下,如何判断某个 是不是核函数?
答案: 是 是核函数当且仅当对任意数据 ,核矩阵(kernal matrix,gram matrix)总是半正定的
知识补充:实对称矩阵
如果有n阶矩阵A,其矩阵的元素都为实数,且矩阵A的转置等于其本身(aij=aji),(i,j为元素的脚标),则称A为实对称矩阵。
知识补充:「正定矩阵」(positive definite)和「半正定矩阵」(positive semi-definite)
正定矩阵: 给定一个大小为 的实对称矩阵 ,若对于任意长度为 的非零向量 ,有 恒成立,则矩阵 是一个正定矩阵。
半正定矩阵: 给定一个大小为 的实对称矩阵 ,若对于任意长度为 的向量 ,有 恒成立,则矩阵 是一个正定矩阵。
半正定矩阵包括了正定矩阵,核矩阵与协方差矩阵都要半正定
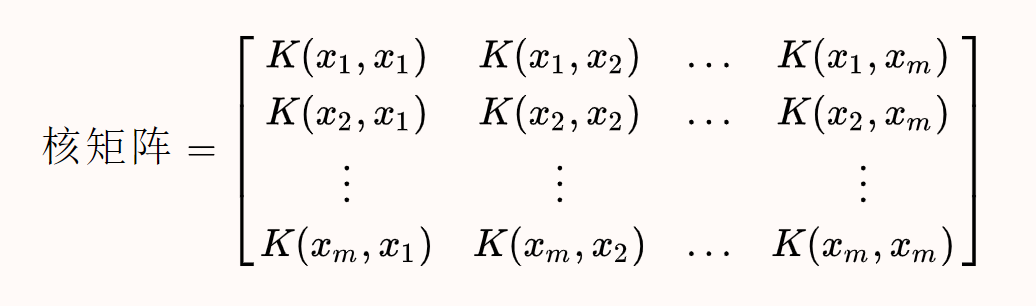
常用核函数

栗子
举一个栗子
下面这张图位于第一、二象限内。我们关注红色的门,以及“北京四合院”这几个字下面的紫色的字母。我们把红色的门上的点看成是“+”数据,紫色字母上的点看成是“-”数据,它们的横、纵坐标是两个特征。显然,在这个二维空间内,“+”“-”两类数据不是线性可分的。

我们现在考虑核函数,即“内积平方”。
这里面是二维空间中的两个点。
这个核函数对应着一个二维空间到三维空间的映射,它的表达式是:
可以验证,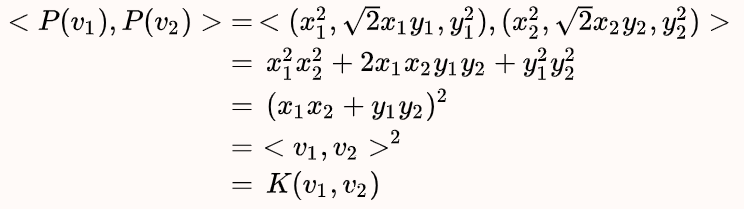
在P这个映射下,原来二维空间中的图在三维空间中的像是这个样子:
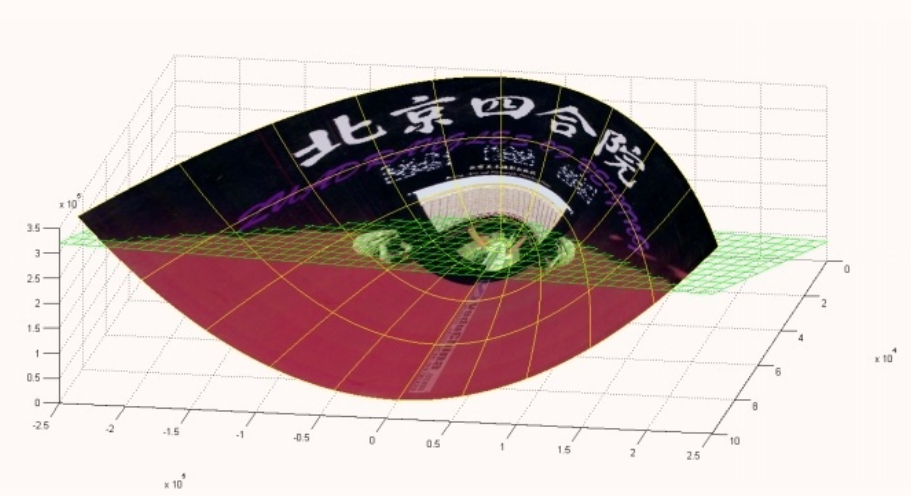
注意到绿色的平面可以完美地分割红色和紫色,也就是说,两类数据在三维空间中变成线性可分的了。
而三维中的这个判决边界,再映射回二维空间中是这样的:

这是一条双曲线,它不是线性的。
通过高维映射使得特征线性可分,换种思路就是当两个特征值无法将数据分开时,就将两个特征值进行点交,形成第三个特征,这个时候就有三个特征值,然后构成三位空间,进行分类










