拟合
理解
对于深度学习或机器学习模型而言,我们不仅要求它对训练数据集有很好的拟合(训练误差),同时也希望它可以对未知数据集(测试集)有很好的拟合结果(泛化能力),所产生的测试误差被称为泛化误差。度量泛化能力的好坏,最直观的表现就是模型的过拟合(overfitting)和欠拟合(underfitting)。过拟合和欠拟合是用于描述模型在训练过程中的两种状态。一般来说,训练过程会是如下所示的一个曲线图。
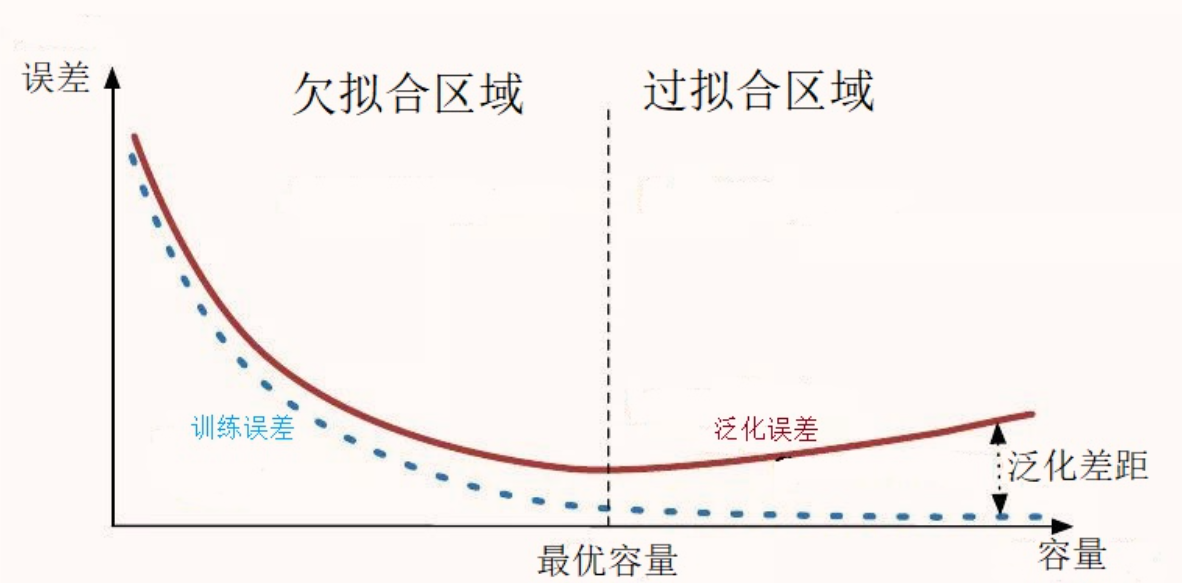
训练刚开始的时候,模型还在学习过程中,处于欠拟合区域。随着训练的进行,训练误差和测试误差都下降。在到达一个临界点之后,训练集的误差下降,测试集的误差上升了,这个时候就进入了过拟合区域——由于训练出来的网络过度拟合了训练集,对训练集以外的数据却不有效。
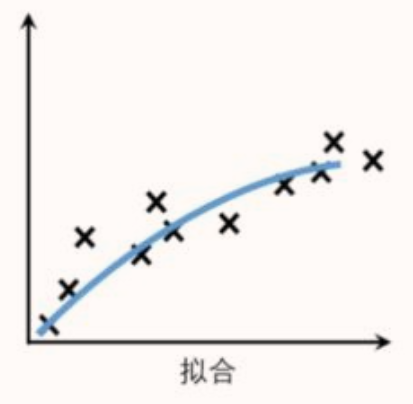
欠拟合
欠拟合是指模型不能在训练集上获得足够低的误差。换句换说,就是模型复杂度低,模型在训练集上就表现很差,没法学习到数据背后的规律。
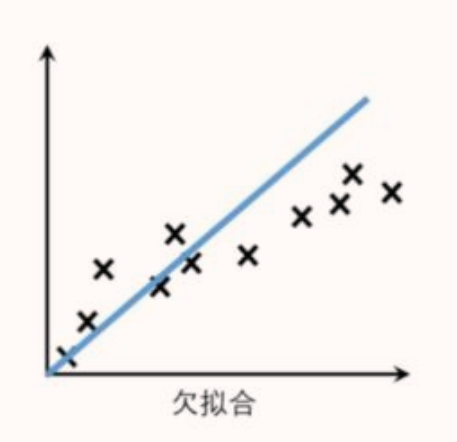
如何解决欠拟合?
欠拟合基本上都会发生在训练刚开始的时候,经过不断训练之后欠拟合应该不怎么考虑了。但是如果真的还是存在的话,可以通过增加网络复杂度或者在模型中增加特征,这些都是很好解决欠拟合的方法。
过拟合
过拟合是指训练误差和测试误差之间的差距太大。换句换说,就是模型复杂度高于实际问题,模型在训练集上表现很好,但在测试集上却表现很差。模型对训练集”死记硬背”(记住了不适用于测试集的训练集性质或特点),没有理解数据背后的规律,泛化能力差。

出现原因
- 训练数据集样本单一,样本不足。 如果训练样本只有负样本,然后那生成的模型去预测正样本,这肯定预测不准。所以训练样本要尽可能的全面,覆盖所有的数据类型。
- 训练数据中噪声干扰过大。 噪声指训练数据中的干扰数据。过多的干扰会导致记录了很多噪声特征,忽略了真实输入和输出之间的关系。
- 模型过于复杂。模型太复杂,已经能够“死记硬背”记下了训练数据的信息,但是遇到没有见过的数据的时候不能够变通,泛化能力太差。我们希望模型对不同的模型都有稳定的输出。模型太复杂是过拟合的重要因素。
如何防止过拟合
要想解决过拟合问题,就要显著减少测试误差而不过度增加训练误差,从而提高模型的泛化能力。我们可以使用正则化(Regularization)方法。
正则化是指修改学习算法,使其降低泛化误差而非训练误差。
正则化方法
常用的正则化方法根据具体的使用策略不同可分为:
(1)直接提供正则化约束的参数正则化方法,如L1/L2正则化;
(2)通过工程上的技巧来实现更低泛化误差的方法,如提前终止(Early stopping)和Dropout;
(3)不直接提供约束的隐式正则化方法,如数据增强等。
- 获取和使用更多的数据(数据集增强)——解决过拟合的根本性方法
让机器学习或深度学习模型泛化能力更好的办法就是使用更多的数据进行训练。但是,在实践中,我们拥有的数据量是有限的。解决这个问题的一种方法就是创建“假数据”并添加到训练集中——数据集增强。通过增加训练集的额外副本来增加训练集的大小,进而改进模型的泛化能力。
- 采用合适的模型(控制模型的复杂度)
过于复杂的模型会带来过拟合问题。对于模型的设计,目前公认的一个深度学习规律”deeper is better”。国内外各种大牛通过实验和竞赛发现,对于CNN来说,层数越多效果越好,但是也更容易产生过拟合,并且计算所耗费的时间也越长。
根据奥卡姆剃刀法则:在同样能够解释已知观测现象的假设中,我们应该挑选“最简单”的那一个。对于模型的设计而言,我们应该选择简单、合适的模型解决复杂的问题。
- 降低特征的数量
对于一些特征工程而言,可以降低特征的数量——删除冗余特征,人工选择保留哪些特征。这种方法也可以解决过拟合问题。
- L1 / L2 正则化
- L1正则化
L1正则化可以使得参数稀疏化,即得到的参数是一个稀疏矩阵,可以用于特征选择。
稀疏性,说白了就是模型的很多参数是0。通常机器学习中特征数量很多,例如文本处理时,如果将一个词组(term)作为一个特征,那么特征数量会达到上万个(bigram)。在预测或分类时,那么多特征显然难以选择,但是如果代入这些特征得到的模型是一个稀疏模型,很多参数是0,表示只有少数特征对这个模型有贡献,绝大部分特征是没有贡献的,即使去掉对模型也没有什么影响,此时我们就可以只
在原始的损失函数后面加上一个L1正则化项,即全部权重 $w$ 的绝对值的和,再乘以λ/n。则损失函数变为:
对应的梯度(导数):
其中 只是简单地取 $w1$ 各个元素地正负号。
梯度下降时权重 $w$ 更新变为:
当 $w=0$ 时,|w|是不可导的。所以我们仅仅能依照原始的未经正则化的方法去更新 $w$ 。
当 $w>0$ 时,sgn( $w$ )>0, 则梯度下降时更新后的 $w$ 变小。
当 $w<0$ 时,sgn( $w$ )>0, 则梯度下降时更新后的 $w$ 变大。换句换说,L1正则化使得权重 $w$ 往0靠,使网络中的权重尽可能为0,也就相当于减小了网络复杂度,防止过拟合。
这也就是L1正则化会产生更稀疏(sparse)的解的原因。此处稀疏性指的是最优值中的一些参数为0。L1正则化的稀疏性质已经被广泛地应用于特征选择机制,从可用的特征子集中选择出有意义的特征。
- L2 正则化
L2正则化可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合。
拟合过程中通常都倾向于让权值尽可能小,最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单,能适应不同的数据集,也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程,若参数很大,那么只要数据偏移一点点,就会对结果造成很大的影响;但如果参数足够小,数据偏移得多一点也不会对结果造成什么影响,专业一点的说法是抗扰动能力强。
L2正则化通常被称为权重衰减(weight decay),就是在原始的损失函数后面再加上一个L2正则化项,即全部权重 $w$ 的平方和,再乘以λ/2n。则损失函数变为:
对应的梯度(导数):
能够发现L2正则化项对偏置 b 的更新没有影响,可是对于权重 $w$ 的更新有影响:
这里的、 $n$ 、都是大于0的, 所以 小于1。因此在梯度下降过程中,权重 $w$ 将逐渐减小,趋向于0但不等于0。这也就是权重衰减(weight decay)的由来。
L2正则化起到使得权重参数 $w$ 变小的效果,为什么能防止过拟合呢?因为更小的权重参数 意味着模型的复杂度更低,对训练数据的拟合刚刚好,不会过分拟合训练数据,从而提高模型的泛化能力。
- Dropout
Dropout是在训练网络时用的一种技巧(trike),相当于在隐藏单元增加了噪声。Dropout 指的是在训练过程中每次按一定的概率(比如50%)随机地“删除”一部分隐藏单元(神经元)。所谓的“删除”不是真正意义上的删除,其实就是将该部分神经元的激活函数设为0(激活函数的输出为0),让这些神经元不计算而已。
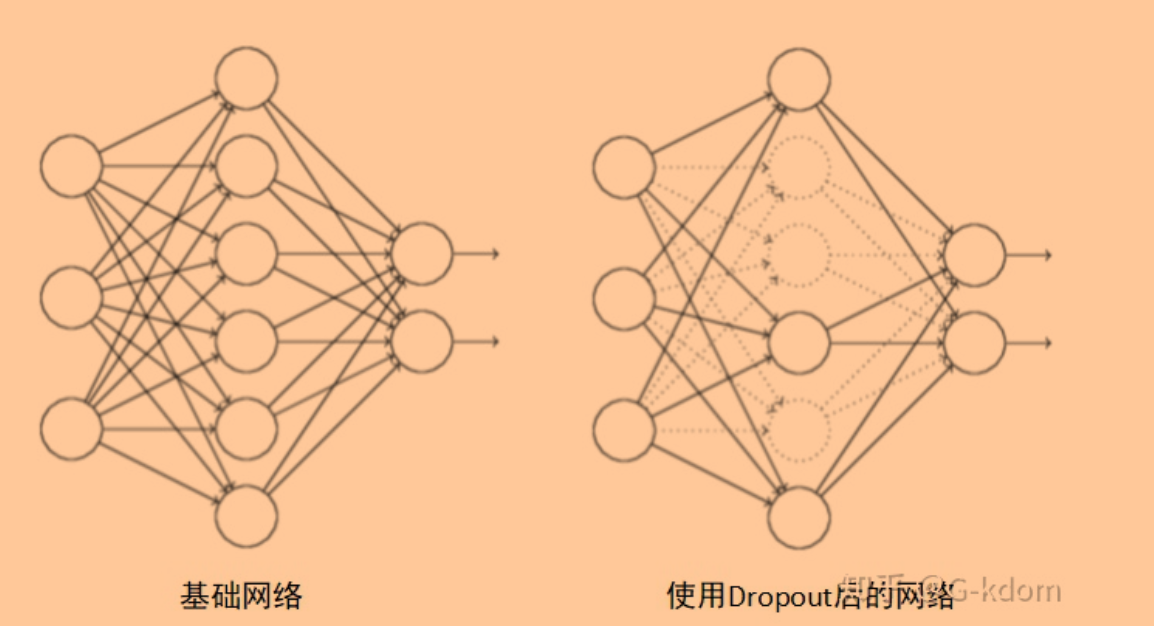
Dropout为什么有助于防止过拟合呢?
(a)在训练过程中会产生不同的训练模型,不同的训练模型也会产生不同的的计算结果。随着训练的不断进行,计算结果会在一个范围内波动,但是均值却不会有很大变化,因此可以把最终的训练结果看作是不同模型的平均输出。
(b)它消除或者减弱了神经元节点间的联合,降低了网络对单个神经元的依赖,从而增强了泛化能力。
理解
通过加入噪声,在训练模型时,扩展模型的接受范围,避免过拟合
- Early stopping(提前终止)
对模型进行训练的过程即是对模型的参数进行学习更新的过程,这个参数学习的过程往往会用到一些迭代方法,如梯度下降(Gradient descent)。Early stopping是一种迭代次数截断的方法来防止过拟合的方法,即在模型对训练数据集迭代收敛之前停止迭代来防止过拟合。
为了获得性能良好的神经网络,训练过程中可能会经过很多次epoch(遍历整个数据集的次数,一次为一个epoch)。如果epoch数量太少,网络有可能发生欠拟合;如果epoch数量太多,则有可能发生过拟合。Early stopping旨在解决epoch数量需要手动设置的问题。具体做法:每个epoch(或每N个epoch)结束后,在验证集上获取测试结果,随着epoch的增加,如果在验证集上发现测试误差上升,则停止训练,将停止之后的权重作为网络的最终参数。
为什么能防止过拟合?
当还未在神经网络运行太多迭代过程的时候,w参数[误差]接近于0,因为随机初始化w值的时候,它的值是较小的随机值。当你开始迭代过程,w的值会变得越来越大。到后面时,w的值已经变得十分大了。所以early stopping要做的就是在中间点停止迭代过程。我们将会得到一个中等大小的w参数,会得到与L2正则化相似的结果,选择了w参数较小的神经网络。
Early Stopping缺点
没有采取不同的方式来解决优化损失函数和过拟合这两个问题,而是用一种方法同时解决两个问题 ,结果就是要考虑的东西变得更复杂。之所以不能独立地处理,因为如果你停止了优化损失函数,你可能会发现损失函数的值不够小,同时你又不希望过拟合。










