用于业务流程事件和结果预测的混合模型

摘要

目的

对于多样性流程进行异常预测

解决

序列k近邻法（KNN）
基于序列比对的马尔科夫模型扩展法

思路：
利用数据的时间分类特征，利用高阶马尔可夫模型预测过程的下一步，并利用序列对比技术预测过程的结果。通过考虑基于k个最近邻的相似过程序列的子集，增加了数据的多样性方面。

结果

已经证明，通过一组实验，序列k最近邻提法比原始提供更好的结果;我们的扩展马尔可夫模型优于随机猜测、马尔可夫模型和隐马尔可夫模型。

知识补充
KNN（K近邻法 K Nearest Neighbors） | 吾辈之人，自当自强不息！
Markov Model（马尔可夫模型） | 吾辈之人，自当自强不息！

阐述

在进行流程预测的前，我们需要从日志中挖掘流程。通过分析数据，可以得知数据为带有时间序列的数据。1999年已经有人证明MMs适用于研究用户网上浏览行为。同时事件序列也可用于训练已经编码后续事件之间的转换概率的马尔可夫模型，
类似其它机器学习模型，越是高阶的模型越是拟合数据，预测结果也更加准确。

知识补充
在马尔可夫链的每一步，系统根据概率分布，可以从一个状态变到另一个状态,也可以保持当前状态。状态的改变叫做过渡，与不同的状态改变相关的概率叫做过渡概率
TODO 默认预测的提出没有仔细研究
当给定数据集很少时，导致无法机器学习和准确预测，所以为了解决这个问题，提出了几个为了解决特征和默认事件之间的非线性依赖关系的模型，通过补充特征默认值来补充数据，进行预测。默认预测

但是当数据多样化同时不聚集的时候，会导致高阶模型弱覆盖，对于未被覆盖的序列，就需要默认预测。但是默认预测会降低模型的准确度。
在马尔可夫模型中，为了平衡覆盖与准确性，一般解决思想是合并多个不同阶的MMs的转换状态，然后在预测的时候遵循“冗余”状态。例如可选择马尔可夫模型（selective Markov model）

TODO
遵循“冗余”状态的实际意义是什么？它的实际表现是什么
an extension of All Kth order Markov models (Deshpande & Karypis, 2004)

知识补充
个人理解弱覆盖是由于特征广而弱，无法高效学习，导致有一些特征被丢弃没有学习到。

第二部部分讲述的是采用kNN算法来预测过程结果，即通过比对给定领域内的序列，找到最相似的序列。06年有研究者发表“预测使用电信公司的数据流失”，用欧几里德距离来计算给定序列与样本之间的距离。

TODO 生物顺序结合没懂

在本文中作者将KNN与生物学的序列对齐组合形成顺序kNN。

知识补充
编辑距离是针对二个字符串（例如英文字）的差异程度的量化量测，量测方式是看至少需要多少次的处理才能将一个字符串变成另一个字符串。

creation

TODO 不理解下面的匹配机制

首先是为了解决高阶MMs弱覆盖，提出了MMs和序列对准融合的技术。当预测模型无法找到预测实例对应的序列时，应用匹配过程以便从与给定序列中最相似的转换矩阵中提取那些序列（图案）。

其次是提出一种预测结果的序列kNN方法，即通过比对序列局部结果，然后比对相似程度，获得预测结果

序列比对

为了确定序列相似性
序列比对主要类似于生物学中的新的DNA序列与DNA数据库进行比较。将DNA序列的事务与蛋白质数据库进行比较，以验证它们之间的关系是否可能发生在发生概率之间。

序列比对
包括全局比对和局部比对
全局比对是提供了全局优化解决方案，遍历所有查询序列的整个长度。
局部比对旨在从两个查询序列中找到最相似的段

我们在MMs中并不是使用当前的序列比对算法，而是使用序列比对的思想；同时作者提出局部序列比对与kNNs的结合使用方法：【替换矩阵】

知识补充
在序列比对算法中的替换矩阵又称为打分矩阵，其数学本质是统计权重。
替换矩阵（计分矩阵）| 原理和作用 - 知乎
在序列比对中，我们一般需要给出一个定量的数值来描述两者的一致性和相似性。在此过程中，替换矩阵用来评价碱基或残基之间的相似性，在长期实践中，人们发现一些特定的碱基替换或者残基替换的频率是要高于另一些替换的，因此人们可以通过统计方法或者基于进化的突变模型来给每一种替换定义不同的分值，来体现出不同碱基或残基之间发生替换的可能性。其可以分成核酸序列替换矩阵和蛋白质序列替换矩阵。

替换矩阵：
生物学中用于描述单位时间内，一个氨基酸转换为另一个氨基酸的速率。本文中替换矩阵作为单位矩阵，主对角线的元素是1，其他元素都是0。为了呈现突变，使用了更复杂形式的替代矩阵。上边知识补充中提到不同的矩阵不同值可以更好表现序列单元之间转换的可能性与频率。我的理解是序列对比的权重表。

打分矩阵
即模型打分矩阵函数：

初始化

计算公式
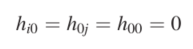
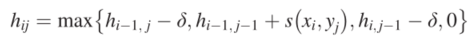
$s (x_{i}, y_{j})$ 是替换矩阵中Xi与Yj的替换分数。
TODO 公式中有个别参数读不懂

案例：
序列ABCDE与序列EBCAD对应的打分矩阵，根据分数高低来寻找最佳片段，然后沿着对角线从最高点到左上角，直至分数为0，来确定匹配序列，如图栗子中为BC。

预测模型

前提：
本模型目的是在流程实例中预测 $s_{i}^{(N + 1)}$ 下一事件 $s_{i + 1}^{(N + 1)}$ 。其中 $S_{N + 1}$ 业务流程中的事件的预测是基于 $S = {S_{1}, S_{2} \dots S_{N}}$

其中一个业务流程实例（Sj）是按时间顺序排列的离散事件(或任务)的组合Sj=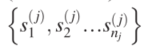 enter description here ，而单个事件是来自于事件类型的有限集合 $E = {e_{1}, \dots, e_{L}}$

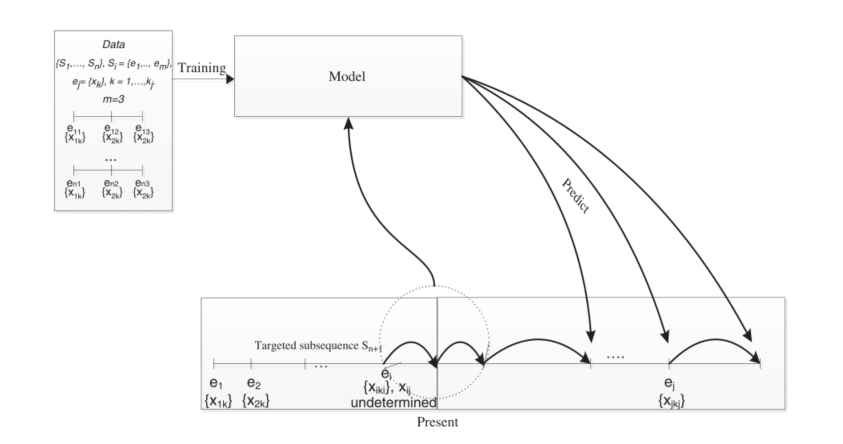
predict model

MMs

Markov Model（马尔可夫模型） | 吾辈之人，自当自强不息！

同时文中为了保障预测模型准确性，提出构建 动态MMs ，通过存储单个事件在数据集中的次数、紧跟事件发生的下一个事件在数据集中的次数（事件A的下一个事件为B，这里指B的次数）和转换矩阵。还可以通过将折扣因子与事件数量结合，这样就可以在加入新数据时更新折扣因子来提供更多权重。

知识补充 折扣因子
(95 封私信 / 79 条消息) 马尔可夫决策过程中为什么需要discount factor ，也就是问为啥时间近的状态影响越大？ - 知乎
 #David Silver Reinforcement Learning # 笔记2-MDP - 简书
 强化学习笔记1 - Hiroki - 博客园

HMM

Markov Model（马尔可夫模型） | 吾辈之人，自当自强不息！

混合模型

主要是平衡准确性和覆盖

结合高阶MMs与序列比对技术（Waterman 1994），以保持高阶马尔可夫模型的高精度，同时弥补缺乏覆盖面积【个人感觉是通过通过增加区别序列对比消除过拟合】，提出了MSA（Markov sequence alignment 马尔可夫序列比对）【一种基于相似序列可能产生相同结果的假设，指处理没有遇到过的新的序列，然后在转换矩阵中找最类似的】

通过构建矩阵比较两个序列的重量，最小则最为接近。
规则：
节点事件相同，则重量为0
如果事件不同则为1或者 $δ$

从两个序列中删除的第一事件A和E导致重量为1
两个序列中的第二个事件是B并且具有重量0
第四个事件A从EBCAD中删除，以便将两个D事件匹配在两个序列中的第四和第五位置，重量加 $δ$
最后，我们从ABCDE序列中删除最后一个事件E，增加重量 $δ$
匹配两个序列的总重量是 $w = 1 + 0 + 0 + δ + δ = 1 + 2δ$

以下示例将说明我们的方法，通过一个三阶MMs的转换矩阵和序列BCC。此序列尚未发生在矩阵之前并未存储在矩阵中。目的是从矩阵找到最相似的序列，并使用它们的预测来为给定序列BCC生成预测。

替换矩阵

我们首先将BCC与ABC相匹配

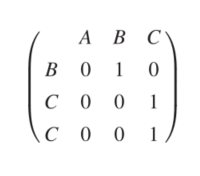
BCC to ABC

weight： $w=δ+0+δ=2δ$

类似地，匹配CBC和BCC的得到的重量

weight: $w=2δ$

BAA和BCC

weight: $w=2$

这一块理解的是当无法通过删除操作达到序列匹配的时候则加重为1，否则通过删除和插入惩罚达 $δ$ 到序列匹配，文中提到的是0.4。
通过比重，ABC与CBC一样小，所以ABC与CBC都和BCC最相似，但是它们的预测载体分别是（0.1,0.2,0.7）和（0.1,0.5,0.4），基于这些向量，就是预测{B，C}的下一步。
这两个事件的发生的权重和频率是相等的;因此，由于两个序列中较高的转换概率分别是 $m _ { 13 }=0.7$ 和 $m _ { 22 }=0.5$ ，因此给定的序列预测的下一步是具有更高的转移概率C。

算法一

比对序列，识别通过删除/插入符号匹配两个序列的最佳编辑过程

算法二
2. 计算匹配两个序列的分数

算法1和2说明了通过删除和插入惩罚来匹配两个序列的过程

KNN结合序列比对

KNN基本上是一种非参数方法;因此，其中一个优点是不需要训练模型。序列KNN的核心思想是**找到类似的序列** ，期望这些序列具有共同的行为和结果。
业务流程的比对需要加入时间特征，这里采用生物学的序列对准技术结合KNN，通过与序列对准组合，kNN允许我们顺序地比较符号序列，提出了K最近序列比对（KnsSA）。

首先根据给的N个序列，构建了距离矩阵 $( d _ { i j } ) N * N$ ，然后使用距离矩阵的元素对序列进行排序。通过使用局部对齐匹配每对序列来获得距离矩阵的元素

评估

过程分析和数据预处理

确定了MSA（Markov sequence alignment 马尔可夫序列比对）和KnsSA（KNN序列比对）

非对应知识补充：MSA
序列两两比对算法_多重序列比对(MSA)分析工具怎么选，看这一篇就够了_weixin_39569389的博客-CSDN博客
 【陪你学·生信】九、多序列比对-Multiple Sequence Alignment（MSA） - 简书

非对应知识补充：MSA
替代梯度下降——基于极大值原理的深度学习训练算法 - 知乎
MSA可以替代梯度下降函数
优一：MSA的每次迭代的收敛速度确实比梯度下降方法快一些
优二：梯度下降法的一大问题就是如果参数初始化得不好，那么就有可能会遇到一些局部平坦的区域，导致收敛速度变慢，而MSA方法则不会受到这个问题的影响
缺点：每轮迭代的时间会比梯度下降慢得多，这是可以理解的，毕竟MSA的每轮迭代都需要去找到一个最大值，而梯度下降只需要计算一次梯度就行了。这就导致了虽然MSA每次迭代收敛地更快，但是从时间上来看却反而更慢了

第一个数据集（DS1）由电信线路故障修复记录为9个月。第二（DS2）涵盖1个月的时间，并表示固定宽带断层的过程。第三数据集DS3来自不同的故障修复过程。数据集DS1和DS2用于我们扩展马尔可夫模型的实验中。数据集DS3和DS4用于KNSSA实验。

数据复杂且长短不一。【文中没有提到整理数据方式，只是进行可视化】

通过工具Aperture挖掘10%的DS1的数据形成的可视化

扩展马尔可夫模型实验

扩展马尔可夫模型实验

RM - 随机模型

为了找到当前之后的下一个任务，我们随机从潜在的下一个任务中选择。例如，从历史数据得知事件a来自于序列A属于集合{C，D，E}的任务，我们随机选择从该设置的值作为预测的下一步。【不通，反正就是一个baseline，在有限的范围内进行下一步】

高阶MMs

从一阶到kth阶生成许多不同的秩马尔可夫模型。给定序列，我们从最高阶MMs开始。如果在转换矩阵中找不到给定序列，我们通过删除序列中的第一个事件来创建新的较短序列。然后，我们将使用下一个下阶MMs继续过程，直到我们在转换矩阵中找到一个匹配项，或者在尝试第一阶Markov模型之后，需要默认预测。【只通过降阶来预测所有序列】

我们测试了几个具有不同长度的多个序列HMM，用于输入序列和不同数量的隐藏状态，并选择了最佳状态。

**结果分析对比**：
90%用于训练，10%做预测。使用十折交叉验证预测结果

知识补充交叉验证
8. Sklearn — 交叉验证(Cross-Validation) - 知乎

首先是构建一阶到七阶MSAs，然后通过通过MSAs选取数据集的最适合 $l$ ,其中DS1取值为5，DS2取值3。

$l$ 表示序列选取长度

下图一，二别说明了DS1和DS2这两个数据集的MSAa准确性。结果表明，通过引入默认预测改进模块，MSA优于其他可比模型，尤其是当马尔可夫模型的阶数增加时。这是因为 序列之间比较的相关性与其长度成正比。

数字表示阶层
蓝色表示原生MMs的预测准确度，红加蓝表示加上默认预测模块改进后的预测精确度。

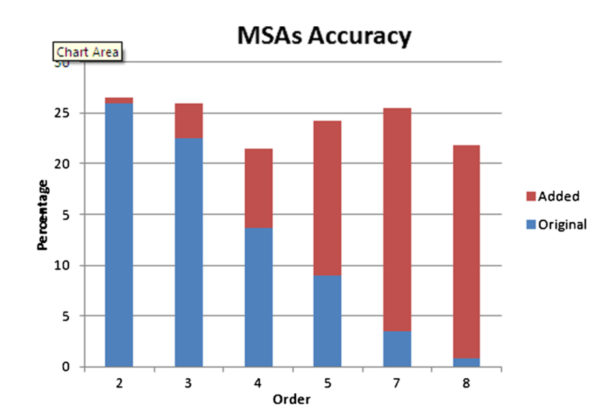
图一，使用数据集DS1在MMs中应用默认预测模块前后的正确预测百分比

图二，使用数据集DS2在MMs中应用默认预测模块前后的正确预测百分比

分析：
二阶MSAs在一系列不同阶MSAs中表现最好，就DS1而言，正确预测27%；三阶MSAs在DS2中表现最好，可以达到70%的准确率。同时可以分析得到在五阶MSAs预测时，默认预测模块的作用明显增加。

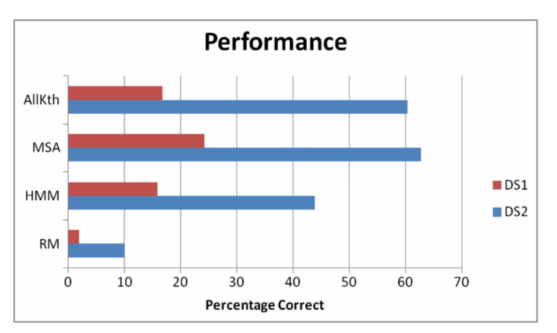
四种模型预测比较，第一个为全阶MMs

这里选择的是五阶段MSA和全五阶MMs，因为全阶段MMs在高阶时是具有优势的，这里为了验证默认预测的作用所以使用五阶。该图显示了两个数据集下所有模型的性能。可以看出，RM表现最差，DS2的成功率只有10%左右。当应用于更大的数据集DS1时，结果下降到接近2%（MSAs是其14倍）。同时可以发现选择正确的下一个任务的概率随着集合大小的增加而降低。结果突出了处理复杂数据集的难度。当数据不是太多样化(即DS2)时，MSA(五阶)获得最高数量的正确预测，结果为63%。与其他基准相比，MSA结果优于达到57%的五阶马尔可夫模型、达到60%的全Kth (K=5)马尔可夫模型和达到43%的隐马尔可夫模型。

连续KNN实验

准备

这块作者提出的预测流程结果，所以需要给数据做标记，用于区分输出结果是成功还是失败。但是不同数据集输出的结果判断标注不同，同一个数据集中不同流程的结果判断标注也不同，这就无法统一对预测结果进行判定。

为了寻找到不同业务流程相统一的结果判断标准，这里采用的是通过设置时间阈值来衡量流程结果的成功与否。

然而，在DS4的情况下，实际交付日期和向客户承诺的交付日期之间的差被用作确定成功和失败的标准。特别是，如果实际交付日期在约定日期之前，则该流程实例被归类为成功，否则被归类为失败。

结果

通过另外两种baseline来评估KnsSA

RM – random model(随机模型)：为了找到过程的结果，我们随机生成一个介于0和1之间的数字；如果生成的数字大于0.5，则结果为成功(1)，反之亦然；如果生成的数字小于0.5，则结果为失败(0)
Original KNN：我们选择K个最近的序列是因为它们有共同的独特任务。例如，给定两个序列A、B、D和A、A、C，第一个序列中有一个A、一个B和一个D；第二个中有两个As和一个C。每个独特的任务可以被视为一个类别。每个类别的距离计算为相应任务出现次数的差值。为了获得任意两个给定序列之间的总距离，对所有类别进行求和。例如，前面给出的两个序列由四个类别A、B、C和D组成。类别A的距离分别为dA= 1，类别B、C和D的距离分别为dB=1、dC=1和dD= 1。这两个序列的总距离为d=dA+dB+dC+dD=4【每个流程中每个事件进行求总距离】

该模型是局部序列比对技术与KNN的结合模型，所以选择KNN的k值，结合实验中标签是0和1，这里作者k值选择为奇数；同时考虑数据集的多样性，k值应该较小。

**知识补充**： k值为什么选择奇数

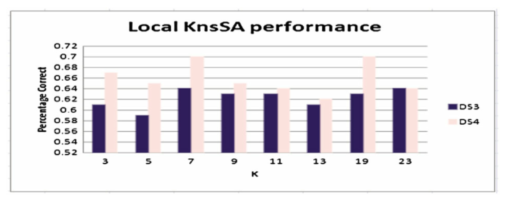
Local KnsSA模型对DS3，DS4预测结果

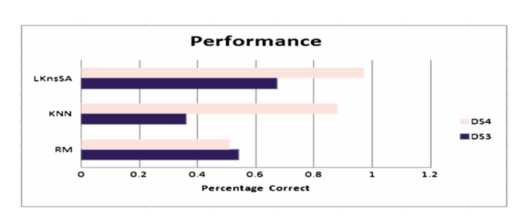
Local KnsSA，KNN，RM对于数据集预测结果

结果表明，该模型优于原始KNN和随机猜测的基准模型。这也意味着数据的时间特性对于预测过程结果很重要。

结论

本文的设计构思，首先通过MMs和HMM生成数据集的替换矩阵，然后作者提出一种序列比对的马尔可夫扩展模型（MSAs）。为了验证该模型的有效性，与MMs和HMMs进行对比，发现其准确率由于其它至少10%。
同时表明了高阶马尔可夫模型预测准确率高于一阶【图五】。从五阶以后加入缺省默认预测模块后可以大幅度提高预测准确度。
第二个贡献是提出新的序列比对KNN（KnsSA）。该方法优于基准模型，证明了数据的序列特征在预测过程结果中的重要作用。相将相似序列进行分类，然后进行下一步处理。