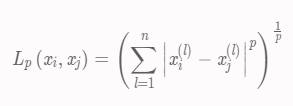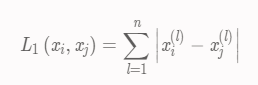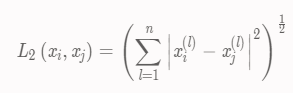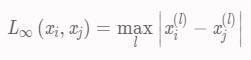KNN(K近邻法 K Nearest Neighbors)
机器学习算法(2)之K近邻算法_不曾走远的博客-CSDN博客
【机器学习】K近邻法(KNN)与kd树原理详解_齐在的专栏-CSDN博客
TODO 序列KNN
KNN概述
- 常用有监督学习方法
- 常用分类方法
- 同时也是回归方法
- 是懒惰学习
扩展学习
懒惰学习是一种训练集处理方法,其会在收到测试样本的同时进行训练,与之相对的是急切学习,其会在训练阶段开始对样本进行学习处理。
基本思路:
如果一个待分类样本在特征空间中的k个最相似(即特征空间中K近邻)的样本中的大多数属于某一个类别,则该样本也属于这个类别,即近朱者赤,近墨者黑。
KNN算法介绍
KNN模型
kNN使用的模型实际上对应于对特征空间的划分。
由三个及基本要素组成:
- 距离度量
- k值的选择
- 决策规划
- 距离度量
KNN中使用的距离度量可以是欧式距离、曼哈顿距离、切比雪夫距离或者一般的闵可夫斯基距离。
知识补充
设特征空间 $X$ 是 $n$ 维实数向量空间,∈ $X$ ,,
闵可夫斯基距离(Minkowski distance,距离)
的距离定义为:
其中,p ≥ 1 。曼哈顿距离(Manhattan distance)
当p = 1 时,距离就变成了曼哈顿距离:欧式距离(Euclidean distance)
当p = 2时,距离就变成了欧式距离:切比雪夫距离(Chebyshev distance)
当距离就变成了切比雪夫距离,它是各个坐标距离的最大值:
- k值选择(借鉴李航–统计学习方法)
如果k值较小,则训练误差减少,只有与输入实例相似的训练实例才会对于预测结果起作用,“学习”近似误差会减小,但泛化误差提高了,预测结果会对近邻实例点非常敏感。k值较小意味着模型变得复杂,容易发生过拟合。
如果k值较大,可以减少泛化误差,其优点是可以减少学习的估计误差,但训练误差会增加,这时与输入实例相差较远的训练实例也会对预测结果起作用。k值较大意味着模型变得简单,容易发生欠拟合。
通常情况下,我们需要对 k 经过多种尝试,来决定到底使用多大的 k 来作为最终参数。k通常会在3~10直接取值,或者是k等于训练数据的平方根。比如15个数据,可能会取k=4。
第二种方法,选择能使测试集达到最优的k kk,即能够使得如MAPE等衡量预测准确度的统计量达到最小;
第三种方法,同时训练多个函数不同参数k kk的模型,然后取所有模型的预测值的平均值作为最终的预测值。
当k = 1时,k近邻算法就是最近邻算法。k值一般采用交叉验证法选取最优值。
- 决策规划
通常,在分类任务中使用投票法计算最终预测结果,在回归任务中使用平均法,还可基于距离远近进行加权平均或加权投票。
KNN算法描述
下面以分类任务为例,介绍KNN算法,回归任务与此类似,区别不大。
输入:训练数据集 ,其中, 是实例的类别。
是实例的类别。
过程:
- 根据给定的距离度量,在训练集D中找出与x最邻近的k个点,涵盖着k 个点的领域记为;
- 在中根据分类决策规则决定x的类别y:
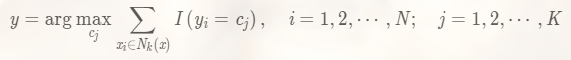
输出:测试样本x xx所属的类别y yy。
KNN算法实现
KNN算法蛮力实现
首先我们看看最想当然的方式。
既然我们要找到k个最近的邻居来做预测,那么我们只需要计算预测样本和所有训练集中的样本的距离,然后计算出最小的k个距离即可,接着多数表决,很容易做出预测。这个方法的确简单直接,在样本量少,样本特征少的时候有效。但是在实际运用中很多时候用不上,为什么呢?因为我们经常碰到样本的特征数有上千以上,样本量有几十万以上,如果我们这要去预测少量的测试集样本,算法的时间效率很成问题。因此,这个方法我们一般称之为蛮力实现。<font color="#1E90FF">比较适合于少量样本的简单模型的时候用</font>。
KD树实现原理
KD树算法没有一开始就尝试对测试样本分类,而是先对训练集建模,建立的模型就是KD树,建好了模型再对测试集做预测。所谓的KD树就是K个特征维度的树,注意这里的K和KNN中的K的意思不同。KNN中的K代表特征输出类别,KD树中的K代表样本特征的维数。为了防止混淆,后面我们称特征维数为n。
KD树算法包括三步,第一步是建树,第二部是搜索最近邻,最后一步是预测。
KD树的建立
我们首先来看建树的方法。KD树建树采用的是从m个样本的n维特征中,分别计算n个特征的取值的方差,用方差最大的第k维特征来作为根节点。对于这个特征,我们选择特征的取值的中位数对应的样本作为划分点,对于所有第k维特征的取值小于的样本,我们划入左子树,对于第k维特征的取值大于等于的样本,我们划入右子树,对于左子树和右子树,我们采用和刚才同样的办法来找方差最大的特征来做根节点,递归的生成KD树。
比如我们有二维样本6个,{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},构建kd树的具体步骤为:
- 找到划分的特征。6个数据点在x,y维度上的数据方差分别为6.97,5.37,所以在x轴上方差更大,用第1维特征建树。
- 确定划分点(7,2)。根据x维上的值将数据排序,6个数据的中值(所谓中值,即中间大小的值)为7,所以划分点的数据是(7,2)。这样,该节点的分割超平面就是通过(7,2)并垂直于:划分点维度的直线x=7;(很显然,中位数为6 ,这里选择(5,4)或者(7,2)都是可以的。这种情况任选一个即可)
- 确定左子空间和右子空间。 分割超平面x=7将整个空间分为两部分:x<=7的部分为左子空间,包含3个节点={(2,3),(5,4),(4,7)};另一部分为右子空间,包含2个节点={(9,6),(8,1)}。
- 用同样的办法划分左子树的节点{(2,3),(5,4),(4,7)}和右子树的节点{(9,6),(8,1)}。最终得到KD树。
- 后续步骤反复上面的,直到两个子区域没有实例存在时停止(这意味着最后所有训练实例都对应一个叶结点或内部结点),从而形成kd树的区域划分。
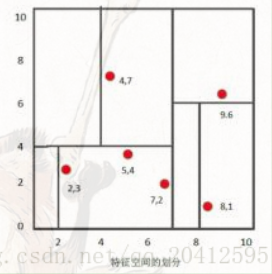
标准kNN算法的切分特征选择是按顺序的,后来对kd树的一个重大改进是选择方差最大的特征,方差越大,不同实例点区分越明显,更方便进行划分。
KD树搜索最近邻
当我们生成KD树以后,就可以去预测测试集里面的样本目标点了。对于一个目标点,我们首先在KD树里面找到包含目标点的叶子节点。以目标点为圆心,以目标点到叶子节点样本实例的距离为半径,得到一个超球体,最近邻的点一定在这个超球体内部。然后返回叶子节点的父节点,检查另一个子节点包含的超矩形体是否和超球体相交,如果相交就到这个子节点寻找是否有更加近的近邻,有的话就更新最近邻。如果不相交那就简单了,我们直接返回父节点的父节点,在另一个子树继续搜索最近邻。当回溯到根节点时,算法结束,此时保存的最近邻节点就是最终的最近邻。
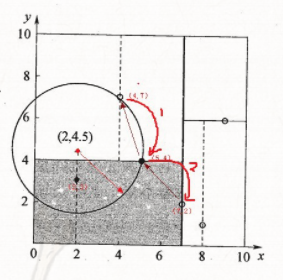
从上面的描述可以看出,KD树划分后可以大大减少无效的最近邻搜索,很多样本点由于所在的超矩形体和超球体不相交,根本不需要计算距离。大大节省了计算时间。
先进行二叉查找,先从(7,2)查找到(5,4)节点,在进行查找时是由y = 4为分割超平面的,由于查找点为y值为4.5,因此进入右子空间查找到(4,7),形成搜索路径<(7,2),(5,4),(4,7)>,但 (4,7)与目标查找点的距离为3.202,而(5,4)与查找点之间的距离为3.041,所以(5,4)为查询点的最近点; 以(2,4.5)为圆心,以3.041为半径作圆,如下图所示。可见该圆和y = 4超平面交割,所以需要进入(5,4)左子空间进行查找,也就是将(2,3)节点加入搜索路径中得<(7,2),(2,3)>;于是接着搜索至(2,3)叶子节点,(2,3)距离(2,4.5)比(5,4)要近,所以最近邻点更新为(2,3),最近距离更新为1.5;回溯查找至(5,4),直到最后回溯到根结点(7,2)的时候,以(2,4.5)为圆心1.5为半径作圆,并不和x = 7分割超平面交割,如下图所示。至此,搜索路径回溯完,返回最近邻点(2,3),最近距离1.5。
球树实现原理
KD树算法虽然提高了KNN搜索的效率,但是在某些时候效率并不高,比如当处理不均匀分布的数据集时,不管是近似方形,还是矩形,甚至正方形,都不是最好的使用形状,因为他们都有角。一个例子如下图: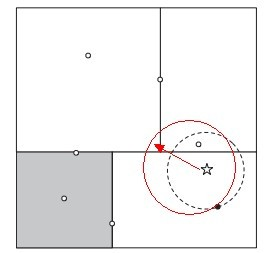
如果黑色的实例点离目标点星点再远一点,那么虚线圆会如红线所示那样扩大,导致与左上方矩形的右下角相交,既然相 交了,那么就要检查这个左上方矩形,而实际上,最近的点离星点的距离很近,检查左上方矩形区域已是多余。于此我们看见,KD树把二维平面划分成一个一个矩形,但矩形区域的角却是个难以处理的问题。
为了优化超矩形体导致的搜索效率的问题,有人引入了球树,这种结构可以优化上面的这种问题。
球树的建立
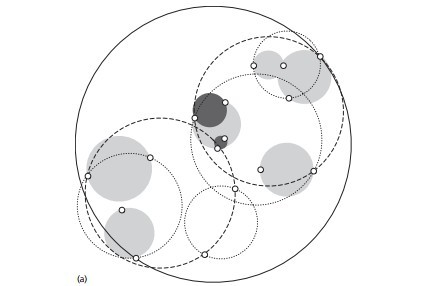
- 先构建一个超球体,这个超球体是可以包含所有样本的最小球体。
- 从球中选择一个离球的中心最远的点,然后选择第二个点离第一个点最远,将球中所有的点分配到离这两个聚类中心最近的一个上,然后计算每个聚类的中心,以及聚类能够包含它所有数据点所需的最小半径。这样我们得到了两个子超球体,和KD树里面的左右子树对应。(PS:这里选择两个点后,就以这两个点来聚类,所以先确定的是以这两个点为中心来计算其他点到该中心的距离。当所有点都确定自己的中心后,再重新计算一次该超球体的半径和球心。)
- 对于这两个子超球体,递归执行步骤2,最终得到了一个球树。
可以看出KD树和球树类似,主要区别在于球树得到的是节点样本组成的最小超球体,而KD得到的是节点样本组成的超矩形体,这个超球体要与对应的KD树的超矩形体小,这样在做最近邻搜索的时候,可以避免一些无谓的搜索。
KNN优缺点
优点:
- 结构简单;
- 无数据输入假定,准确度高,对异常点不敏感。
- 训练时间复杂度比支持向量机之类的算法低,仅为O(n)
- 由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合
缺点:
实战
机器学习(一)——K-近邻(KNN)算法 - Yabea - 博客园
序列KNN
机器学习(二十八)——KNN, AutoML, 数据不平衡问题
R语言实战——基于KNN聚类的时间序列分析预测_三只佩奇不结义的博客-CSDN博客_r语言knn回归及预测
python - 如何使用 KNN/K-means 对数据帧中的时间序列进行聚类 - IT工具网
iwuqing/Time-Series-Classification-based-on-KNN: 基于KNN聚类算法结合Dynamic Time Warping(动态时间调整)的时间序列分类