一次性弄懂马尔可夫模型、隐马尔可夫模型、马尔可夫网络和条件随机场！(词性标注代码实现) - mantch - 博客园

马尔可夫网络、马尔可夫模型、马尔可夫过程、贝叶斯网络的区别

共分六点说明这些概念【这6点是依次递进的，不要跳跃着看】：

  1. 将随机变量作为结点，若两个随机变量相关或者不独立，则将二者连接一条边；若给定若干随机变量，则形成一个有向图，即构成一个网络。
  2. 如果该网络是有向无环图，则这个网络称为贝叶斯网络。
  3. 如果这个图退化成线性链的方式，则得到马尔可夫模型；因为每个结点都是随机变量，将其看成各个时刻(或空间)的相关变化，以随机过程的视角，则可以看成是马尔可夫过程。
  4. 若上述网络是无向的，则是无向图模型，又称马尔可夫随机场或者马尔可夫网络。
  5. 如果在给定某些条件的前提下，研究这个马尔可夫随机场，则得到条件随机场。
  6. 如果使用条件随机场解决标注问题，并且进一步将条件随机场中的网络拓扑变成线性的，则得到线性链条件随机场。

马尔可夫模型

马尔可夫过程

马尔可夫过程（Markov process）是一类随机过程。它的原始模型是马尔可夫链。
该过程具有如下特性：在已知目前状态（现在）的条件下，它未来的演变（将来）不依赖于它以往的演变 (过去 )。

每个状态的转移只依赖于之前的n个状态，这个过程被称为1个n阶的模型，其中n是影响转移状态的数目。最简单的马尔可夫过程就是一阶过程，每一个状态的转移只依赖于其之前的那一个状态，这个也叫作马尔可夫性质。

假设这个模型的每个状态都只依赖于之前的状态，这个假设被称为马尔科夫假设，这个假设可以大大的简化这个问题。显然，这个假设可能是一个非常糟糕的假设，导致很多重要的信息都丢失了。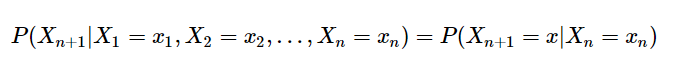

假设天气服从马尔可夫链：

天气

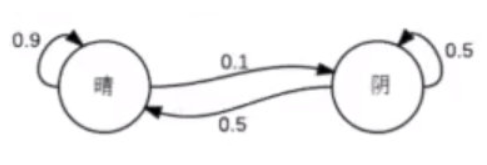
从上面这幅图可以看出：

  • 假如今天是晴天，明天变成阴天的概率是0.1
  • 假如今天是晴天，明天任然是晴天的概率是0.9，和上一条概率之和为1，这也符合真实生活的情况。

表格

由上表我们可以得到马尔可夫链的状态转移矩阵：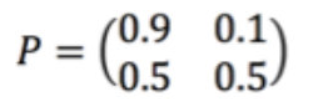
状态转移矩阵

因此，一阶马尔可夫过程定义了以下三个部分：

  • 状态：晴天和阴天
  • 初始向量：定义系统在时间为0的时候的状态的概率
  • 状态转移矩阵：每种天气转换的概率

马尔可夫模型（Markov Model）是一种统计模型，广泛应用在语音识别，词性自动标注，音字转换，概率文法等各个自然语言处理等应用领域。经过长期发展，尤其是在语音识别中的成功应用，使它成为一种通用的统计工具。到目前为止，它一直被认为是实现快速精确的语音识别系统的最成功的方法。

隐马尔可夫模型（HMM）

在某些情况下马尔科夫过程不足以描述我们希望发现的模式。回到之前那个天气的例子，一个隐居的人可能不能直观的观察到天气的情况，但是有一些海藻。民间的传说告诉我们海藻的状态在某种概率上是和天气的情况相关的。在这种情况下我们有两个状态集合，一个可以观察到的状态集合（海藻的状态）和一个隐藏的状态（天气的状况）。我们希望能找到一个算法可以根据海藻的状况和马尔科夫假设来预测天气的状况。

而这个算法就叫做**隐马尔可夫模型(HMM)**。

HMM

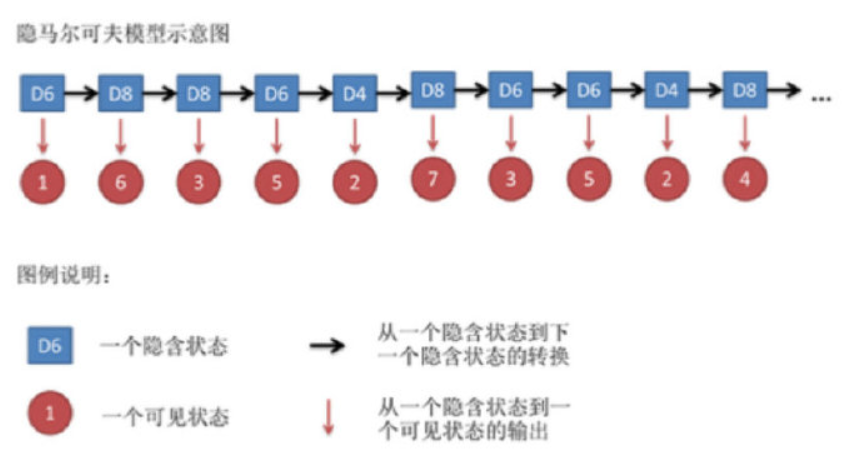
隐马尔可夫模型 (Hidden Markov Model) 是一种统计模型，用来描述一个含有隐含未知参数的马尔可夫过程。它是结构最简单的动态贝叶斯网，这是一种著名的有向图模型， 主要用于时序数据建模，在语音识别、自然语言处理等领域有广泛应用。

隐马尔可夫三大问题

注意

  1. 给定模型，如何有效计算产生观测序列的概率？换言之，如何评估模型与观测序列之间的匹配程度？
  2. 给定模型和观测序列，如何找到与此观测序列最匹配的状态序列？换言之，如何根据观测序列推断出隐藏的模型状态？
  3. 给定观测序列，如何调整模型参数使得该序列出现的概率最大？换言之，如何训练模型使其能最好地描述观测数据？

前两个问题是模式识别的问题：1) 根据隐马尔科夫模型得到一个可观察状态序列的概率(评价)；2) 找到一个隐藏状态的序列使得这个序列产生一个可观察状态序列的概率最大(解码)。第三个问题就是根据一个可以观察到的状态序列集产生一个隐马尔科夫模型（学习）。

对应的三大问题解法：

  1. 向前算法(Forward Algorithm)、向后算法(Backward Algorithm)
  2. 维特比算法(Viterbi Algorithm)
  3. 鲍姆-韦尔奇算法(Baum-Welch Algorithm) (约等于EM算法)

小明现在有三天的假期，他为了打发时间，可以在每一天中选择三件事情来做，这三件事情分别是散步、购物、打扫卫生(对应着可观测序列)，可是在生活中我们所做的决定一般都受到天气的影响，可能晴天的时候想要去购物或者散步，可能下雨天的时候不想出门，留在家里打扫卫生。而天气(晴天、下雨天)就属于隐藏状态，用一幅概率图来表示这一马尔可夫过程：

场景

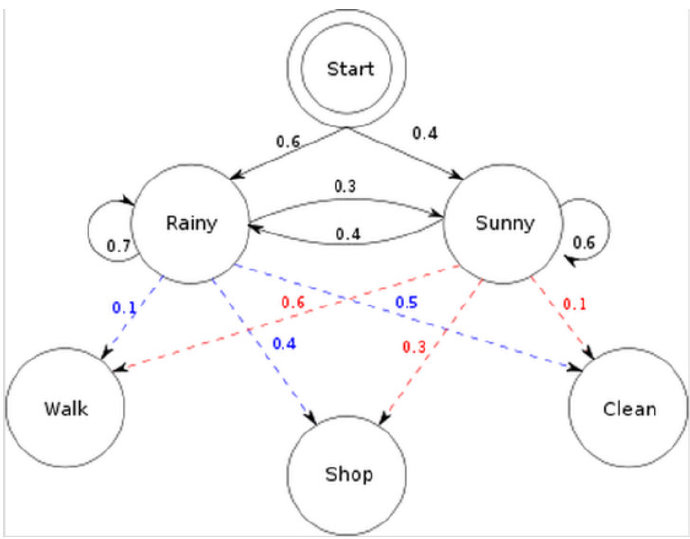
那么，我们提出三个问题，分别对应马尔可夫的三大问题：

  1. 已知整个模型，我观测到连续三天做的事情是：散步，购物，收拾。那么，根据模型，计算产生这些行为的概率是多少。
  2. 同样知晓这个模型，同样是这三件事，我想猜，这三天的天气是怎么样的。
  3. 最复杂的，我只知道这三天做了这三件事儿，而其他什么信息都没有。我得建立一个模型，晴雨转换概率，第一天天气情况的概率分布，根据天气情况选择做某事的概率分布。

第一个问题解法

  1. 遍历算法

假设第一天(T=1 时刻)是晴天，想要购物，那么就把图上的对应概率相乘就能够得到了。
第二天(T=2 时刻)要做的事情，在第一天的概率基础上乘上第二天的概率，依次类推，最终得到这三天(T=3 时刻)所要做的事情的概率值，这就是遍历算法，简单而又粗暴。但问题是用遍历算法的复杂度会随着观测序列和隐藏状态的增加而成指数级增长。

复杂度为：2TNT

理解：每次计算行为发生概率都从最开始遍历计算

  1. 前向算法

    1. 假设第一天要购物，那么就计算出第一天购物的概率(包括晴天和雨天)；假设第一天要散步，那么也计算出来，依次枚举。
    2. 假设前两天是购物和散步，也同样计算出这一种的概率；假设前两天是散步和打扫卫生，同样计算，枚举出前两天行为的概率。
    3. 第三步就是计算出前三天行为的概率。

第二步中要求的概率可以在第一步的基础上进行，同样的，第三步也会依赖于第二步的计算结果。那么这样做就能够节省很多计算环节，类似于动态规划。

复杂度为：N2T

  1. 后向算法

跟前向算法相反，我们知道总的概率肯定是1，那么B_t=1，也就是最后一个时刻的概率合为1，先计算前三天的各种可能的概率，在计算前两天、前一天的数据，跟前向算法相反的计算路径。

第二个问题解法

  1. 维特比算法（Viterbi）

维特比算法是一个特殊但应用最广的动态规划算法。利用动态规划，可以解决任何一个图中的最短路径问题。而维特比算法是针对一个特殊的图—篱笆网络（Lattice）的有向图最短路径问题而提出的。它之所以重要，是因为凡是使用隐含马尔可夫模型描述的问题都可以用它来解码，包括今天的数字通信、语音识别、机器翻译、拼音转汉字、分词等。

维特比算法一般用于模式识别，通过观测数据来反推出隐藏状态。

因为是要根据观测数据来反推，所以这里要进行一个假设，假设这三天所做的行为分别是：散步、购物、打扫卫生，那么我们要求的是这三天的天气(路径)分别是什么。

  1. 初始计算第一天下雨和第一天晴天去散步的概率值：
    △1(R)表示第一天下雨的概率
    πR表示中间的状态(下雨)概率
    bR(O1=w)表示下雨并且散步的概率
    aR-R表示下雨天到下雨天的概率

△1(R)=πR*bR(O1=w)=0.6 * 0.1 = 0.06

△1(S)=πS*bS(O1=w)=0.4 * 0.6 = 0.24

初始路径为：
ϕ1(R)=Rainy
ϕ1(S)=Sunny

  1. 计算第二天下雨和第二天晴天去购物的概率值:

行为概率

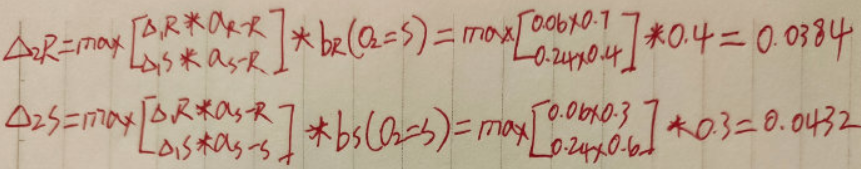
对应路径为：

对应路径

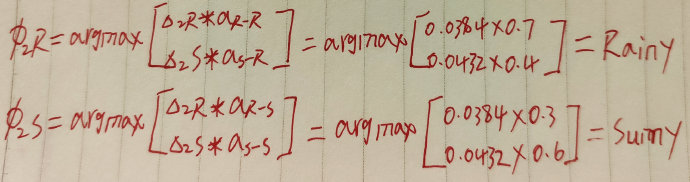
  1. 计算第三天下雨和第三天晴天去打扫卫生的概率值：

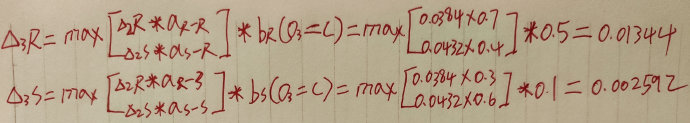
第三天概率

对应路径为：

行为路径

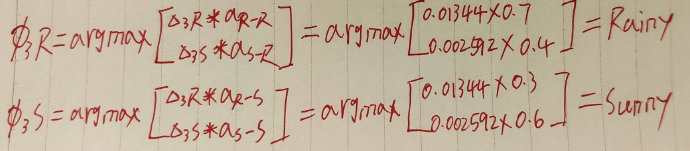
  1. 比较每一步中△的概率大小，选取最大值并找到对应的路径，依次类推就能找到最有可能的隐藏状态路径。

    1. 第一天的概率最大值为 △1S，对应路径为Sunny，
    2. 第二天的概率最大值为 △2S，对应路径为Sunny，
    3. 第三天的概率最大值为 △3S，对应路径为Rainy。

  2. 合起来的路径就是Sunny->Sunny->Rainy，这就是我们所求。

第三个问题解法

鲍姆-韦尔奇算法(Baum-Welch Algorithm) (约等于EM算法)

如果训练数据只有观测序列而没有状态序列，即{O1,O2,⋯,OS}此时HMM的学习就得使用EM算法了，这是非监督学习。

通常，如果给定数据和已经模型，那么求模型参数我们会用极大似然估计法，但是如果变量中含有隐变量，无法用极大似然求解（对数式子里面有求和，难以求出解析解），此时就可以使用EM算法。考虑HMM，观测序列 O是显变量，而状态变量I 则是隐变量，所以HMM实际上是含有隐变量的概率模型

HMM的概率模型 | λ为模型参数

知识补充
极大似然估计
利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！
换句话说，极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。

可以使用EM算法来求得模型参数。

关于EM算法流程，有多个版本，但是仔细学习可以发现是大同小异的，以下使用《统计学习方法》上介绍的EM算法流程。

HMM学习笔记（二）：监督学习方法与Baum-Welch算法_成都往右的博客-CSDN博客

马尔可夫网络

因子图

WiKIpedia：将一个具有多变量的全局函数因子分解，得到几个局部函数的乘积，以此为基础得到的一个双向图叫做因子图（Factor Graph）。

通俗来讲，所谓因子图就是对函数进行因子分解得到的一种概率图。一般内含两种节点：变量节点和函数节点。我们知道，一个全局函数通过因式分解能够分解为多个局部函数的乘积，这些局部函数和对应的变量关系就体现在因子图上。

栗子

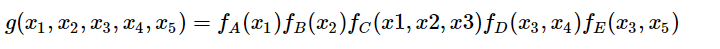
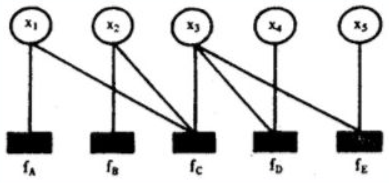
其中fA,fB,fC,fD,fE为各函数，表示变量之间的关系，可以是条件概率也可以是其他关系。其对应的因子图为：

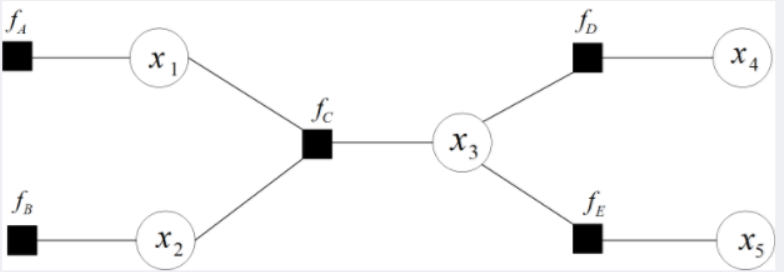
变量-函数之间因子图

变量-函数之间因子图

马尔可夫网络

我们已经知道，有向图模型，又称作贝叶斯网络，但在有些情况下，强制对某些结点之间的边增加方向是不合适的。使用没有方向的无向边，形成了无向图模型（Undirected Graphical Model,UGM）, 又被称为马尔可夫随机场或者马尔可夫网络（Markov Random Field, MRF or Markov network）。

MRF

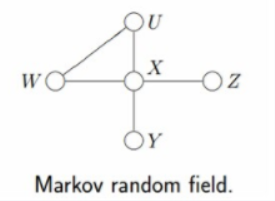
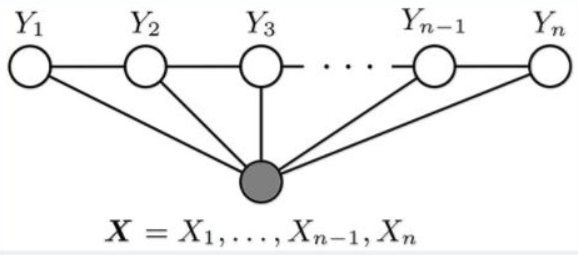
设X=(X1,X2…Xn)和Y=(Y1,Y2…Ym)都是联合随机变量，若随机变量Y构成一个无向图 G=(V,E)表示的马尔可夫随机场（MRF），则条件概率分布P(Y|X)称为条件随机场（Conditional Random Field, 简称CRF，后续新的博客中可能会阐述CRF）。如下图所示，便是一个线性链条件随机场的无向图模型：

CRF

在概率图中，求某个变量的边缘分布是常见的问题。这问题有很多求解方法，其中之一就是把贝叶斯网络或马尔可夫随机场转换成因子图，然后用sum-product算法求解。换言之，基于因子图可以用sum-product 算法高效的求各个变量的边缘分布。

详细的sum-product算法过程，请查看博文：从贝叶斯方法谈到贝叶斯网络_结构之法 算法之道-CSDN博客_贝叶斯

条件随机场(CRF)

一个通俗的例子

假设你有许多小明同学一天内不同时段的照片，从小明提裤子起床到脱裤子睡觉各个时间段都有（小明是照片控！）。现在的任务是对这些照片进行分类。比如有的照片是吃饭，那就给它打上吃饭的标签；有的照片是跑步时拍的，那就打上跑步的标签；有的照片是开会时拍的，那就打上开会的标签。问题来了，你准备怎么干？

一个简单直观的办法就是，不管这些照片之间的时间顺序，想办法训练出一个多元分类器。就是用一些打好标签的照片作为训练数据，训练出一个模型，直接根据照片的特征来分类。例如，如果照片是早上6:00拍的，且画面是黑暗的，那就给它打上睡觉的标签;如果照片上有车，那就给它打上开车的标签。

乍一看可以！但实际上，由于我们忽略了这些照片之间的时间顺序这一重要信息，我们的分类器会有缺陷的。举个例子，假如有一张小明闭着嘴的照片，怎么分类？显然难以直接判断，需要参考闭嘴之前的照片，如果之前的照片显示小明在吃饭，那这个闭嘴的照片很可能是小明在咀嚼食物准备下咽，可以给它打上吃饭的标签；如果之前的照片显示小明在唱歌，那这个闭嘴的照片很可能是小明唱歌瞬间的抓拍，可以给它打上唱歌的标签。

所以，为了让我们的分类器能够有更好的表现，在为一张照片分类时，我们必须将与它相邻的照片的标签信息考虑进来。这——就是条件随机场(CRF)大显身手的地方！这就有点类似于词性标注了，只不过把照片换成了句子而已，本质上是一样的。

如同马尔可夫随机场，条件随机场为具有无向的图模型，图中的顶点代表随机变量，顶点间的连线代表随机变量间的相依关系，在条件随机场中，随机变量Y 的分布为条件机率，给定的观察值则为随机变量 X。下图就是一个线性连条件随机场。

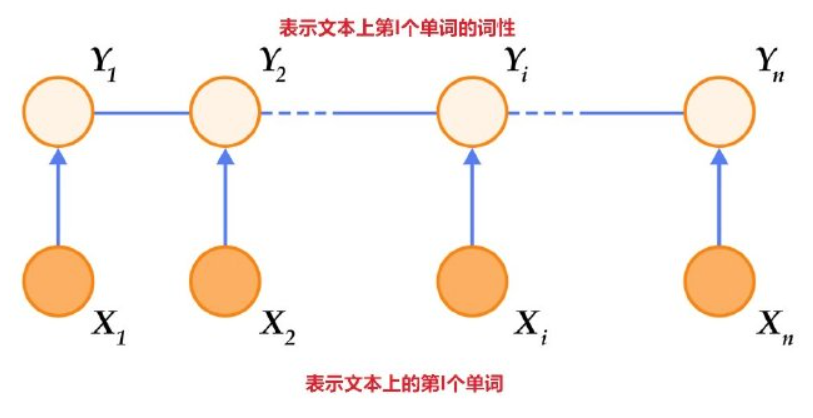
线性连条件随机场

条件概率分布P(Y|X)称为条件随机场。

EM算法、HMM、CRF的比较

  1. EM算法是用于含有隐变量模型的极大似然估计或者极大后验估计，有两步组成：E步，求期望（expectation）；M步，求极大（maxmization）。本质上EM算法还是一个迭代算法，通过不断用上一代参数对隐变量的估计来对当前变量进行计算，直到收敛。注意：EM算法是对初值敏感的，而且EM是不断求解下界的极大化逼近求解对数似然函数的极大化的算法，也就是说EM算法不能保证找到全局最优值。对于EM的导出方法也应该掌握。
  2. 隐马尔可夫模型是用于标注问题的生成模型。有几个参数（π，A，B）：初始状态概率向量π，状态转移矩阵A，观测概率矩阵B。称为马尔科夫模型的三要素。马尔科夫三个基本问题：
    概率计算问题：给定模型和观测序列，计算模型下观测序列输出的概率。–》前向后向算法
    学习问题：已知观测序列，估计模型参数，即用极大似然估计来估计参数。–》Baum-Welch(也就是EM算法)和极大似然估计。
    预测问题：已知模型和观测序列，求解对应的状态序列。–》近似算法（贪心算法）和维比特算法（动态规划求最优路径）
  3. 条件随机场CRF，给定一组输入随机变量的条件下另一组输出随机变量的条件概率分布密度。条件随机场假设输出变量构成马尔科夫随机场，而我们平时看到的大多是线性链条随机场，也就是由输入对输出进行预测的判别模型。求解方法为极大似然估计或正则化的极大似然估计。
  4. 之所以总把HMM和CRF进行比较，主要是因为CRF和HMM都利用了图的知识，但是CRF利用的是马尔可夫随机场（无向图），而HMM的基础是贝叶斯网络（有向图）。而且CRF也有概率计算问题、学习问题和预测问题。大致计算方法和HMM类似，只不过不需要EM算法进行学习问题。
  5. HMM和CRF对比：其根本还是在于基本的理念不同，一个是生成模型，一个是判别模型，这也就导致了求解方式的不同。