强化学习
强化学习读书笔记 - 00 - 术语和数学符号 - SNYang - 博客园
强化学习笔记1 - Hiroki - 博客园
简介
监督学习在机器学习中取得了重大的成功,然而在顺序决策制定和控制问题中,比如无人直升机、无人汽车等,难以给出显式的监督信息,因此这类问题中监督模型无法学习。
强化学习就是为了解决这类问题而产生的。在强化学习框架中,学习算法被称为一个agent,假设这个agent处于一个环境中,两者之间存在交互。agent通过与环境交互不断增强对环境的适应力,故得名强化学习。
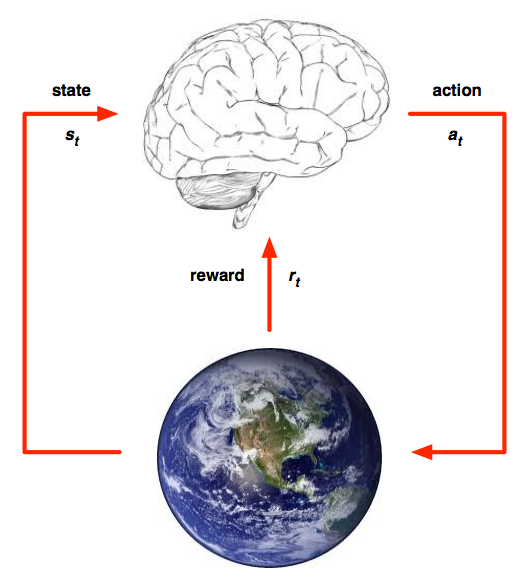
在每个时间步 $t$ ,agent:
- 接受状态 $s _ { t }$
- 接受标量回报 $r _ { t }$
- 执行行动 $a _ { t }$
环境:
- 接受动作 $a _ { t }$
- 产生状态 $s _ { t }$
- 产生标量回报 $r _ { t }$
MDP(马尔科夫决策过程)
通常我们都是从MDP(马尔科夫决策过程)来了解强化学习的。MDP问题中,我们有一个五元组: $( S , A , P , \gamma , P )$
- $S$ :状态集,由agent所有可能的状态组成
- $A$ :动作集,由agent所有可能的行动构成
- $P ( s , a , s ^ { \prime } )$ :转移概率分布,表示状态s下执行动作a后下个时刻状态的概率分布
- $\gamma$ :折扣因子,0≤ $\gamma$ ≤1,表示未来回报相对于当前回报的重要程度。如果 $\gamma$ =0,表示只重视当前立即回报; $\gamma$ =1表示将未来回报视为与当前回报同等重要。【这块不懂,可以看后面下围棋的栗子】
- $R ( s , a , s ^ { \prime } )$ :标量立即回报函数。执行动作a,导致状态s转移到s′产生的回报。可以是关于状态-动作的函数 $S \times A \rightarrow R$ ,也可以是只关于状态的函数 $S \rightarrow R$ 。记t时刻的回报为 $r _ { t }$ ,为了后续表述方便,假设我们感兴趣的问题中回报函数只取决于状态,而状态-动作函数可以很容易地推广,这里暂不涉及。
注: 这里阐述的MDP称为discounted MDP,即带折扣因子的MDP。有些MDP也可以定义为四元组: $( S , A , P , R )$ ,这是因为这类MDP中使用的值函数不考虑折扣因子。
**马尔可夫性质*:当一个随机过程在给定现在状态及所有过去状态情况下,其未来状态的条件概率分布仅依赖于当前状态;换句话说,在给定现在状态时,它与过去状态(即该过程的历史路径)是条件独立的,那么此随机过程即具有马尔可夫性质。
例如:明天的天气(是否下大雨)仅与今天的天气(是否刮大风)有关,而与前天及以前的天气无关*。
MDP过程具有马尔科夫性质,即给定当前状态,未来的状态与过去的状态无关。但与马尔科夫链不同的是,MDP还考虑了动作,也就是说MDP中状态的转移不仅和状态有关,还依赖于agent采取的动作。
我们可以通过下面表格了解各种马尔科夫模型的区别:
| 不考虑动作 | 考虑动作 | |
|---|---|---|
| 状态可观测 | 马尔科夫链(MC) | 马尔科夫决策过程(MDP) |
| 状态不完全可观测 | 隐马尔科夫模型(HMM) | 不完全可观察马尔可夫决策过程(POMDP) |
MDP的运行过程: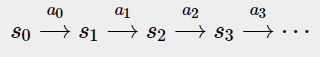
我们从初始状态 $s _ { 0 }$ 出发,执行某个动作 $a _ { 0 }$ ,根据转移概率分布确定下一个状态 $s _ { 1 }$ ∼ $P _ { s0a0 }$ ,接着执行动作 $a _ { 1 }$ ,再根据 $P _ { s1a1 }$ 确定 $s _ { 2 }$ …。
一个discounted MDP中,我们的目标最大化一个累积未来折扣回报:
$R _ { t } = \sum _ { k = 0 } ^ { \infty } \gamma ^ { k } r _ { t + k + 1 }$
具体地,我们希望学得一个策略(policy),通过执行这个策略使上式最大化。策略一般可以表示为一个函数,它以状态为输入,输出对应的动作。策略函数可以是确定的 $\pi ( s ) = a$ ,也可以是不确定的 $\pi ( s , a ) = p ( a | s )$ (这时策略函数是一个条件概率分布,表示给定状态s下执行下一个动作a的概率)。当agent执行一个策略时,每个状态下agent都执行策略指定的动作。
强化学习通常具有延迟回报的特点,以下围棋为例,只有在最终决定胜负的那个时刻才有回报(赢棋为1,输棋为-1),而之前的时刻立即回报均为0。这种情况下, $R _ { t }$ 等于1或-1,这将导致我们很难衡量策略的优劣,因为即使赢了一盘棋,未必能说明策略中每一步都是好棋;同样输了一盘棋也未必能说明每一步都是坏棋。因此我们需要一个目标函数来刻画策略的长期效用。
为此,我们可以为策略定义一个值函数(value function)来综合评估某个策略的好坏。这个函数既可以是只关于状态的值函数 $V ^ { \pi } ( s )$ ,也可以状态-动作值函数 $Q ^ { \pi } ( s , a )$ 。状态值函数评估agent处于某个状态下的长期收益, 动作值函数评估agent在某个状态下执行某个动作的长期收益。
本文后续都将以 状态值函 数为例,进行阐述。一般常用的有三种形式:
- $V ^ { \pi } ( s ) = E _ { \pi } [ \sum _ { k = 0 } ^ { \infty } r _ { t + k + 1 } | s _ { t } = s ]$
- $V ^ { \pi } ( s ) = E _ { \pi } [ \lim _ { k \rightarrow \infty } \frac { 1 } { k } \sum _ { i = 0 } ^ { k } T _ { t + i + 1 } | s _ { t } = s ]$
- $V ^ { \pi } ( s ) = E _ { \pi } [ \sum _ { k = 0 } ^ { \infty } \gamma ^ { k } r _ { t + k + 1 } | s _ { t } = s ]$
其中 $E _ { \pi } [ \cdot | s _ { t } = s ]$ 表示从状态s开始,通过执行策略 $π$ 得到的累积回报的期望。有些情况下,agent和环境的交互是无止境的,比如一些控制问题,这样的问题称为 continuing task 。还有一种情况是我们可以把交互过程打散成一个个 **片段式任务**(episodic task),每个片段有一个起始态和一个终止态(或称为吸收态,absorbing state),比如下棋。当每个episode结束时,我们对整个过程重启随机设置一个起始态或者从某个随机起始分布采样决定一个起始态。
上面三种值函数中,我们一般常用第三种形式,我把它叫做 **折扣值函数**(discounted value function)。











