损失函数之交叉熵(一般用于分类问题)
信息量、信息熵、相对熵
信息量
一件事发生的概率越大,其蕴含的信息量就越少,反之,若发生的几率越小,则蕴含的信息量就越大。
例如,“太阳从东方升起”:这件事发生概率极大,大家都习以为常,所以不觉得有什么不妥的地方,因此蕴含信息量很小。但“国足踢入世界杯”:这就蕴含的信息量很大了,因为这件事的发生概率很小。
若某事x的发生概率为P(x),则信息量的计算公式为:
$I ( x ) = - \log ( P ( x ) )$
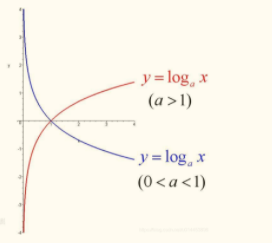
上式的log的底为2,当然也可以是e、10。在神经网络中,log的底一般是e。当log的底大于1,log的图形就像下图红色线。因为P(x)的取值范围为01,可以看到,log的图像,在01的时候是负数,且P(x)越接近0,log越接近负无穷,P(x)越接近1,log越接近0,所以信息量的公式会在log前面加个负号,让log的取值范围为0~∞。当P(x)接近0,log接近无穷,P(x)接近1,log接近0,这符合信息量的概率越小,信息量越大的定义。
信息熵
信息熵可以表达数据的信息量大小。
信息熵也被称为熵,用来表示所有信息量的期望。
期望是试验中每次可能结果的概率乘以其结果的总和。
信息熵的公式如下:
$H ( X ) = - \sum _ { i = 1 } ^ { n } P ( x _ { i } ) \log ( P ( x _ { i } ) )$ $( X = x _ { 1 } , x _ { 2 } , x _ { 3 } , x _ { n - 1 } , x _ { n } )$
使用明天的天气概率来计算其信息熵:

$H ( X ) = - ( 0.5 * \log ( 0.5 ) + 0.2 * \log ( 0.2 ) + 0.3 * \log ( 0.3 ) )$
KL散度(相对熵)—–用于衡量两个概率分布的差异
如何理解 “衡量两个概率分布的差异”?
例如在机器学习中,常常用P(x)表示样本的真实分布,用Q(x)表示模型预测的分布,比如在一个三分类任务中(例如,猫狗马分类器),[x1,x2,x3]分别表示猫,狗,马的概率,输入一张猫的图片,其真实分布为P(x)=[1,0,0],预测分布为Q(x)=[0.7,0.2,0,1],那么P(x)和Q(x)就是两个不同的概率分布,可以用KL散度来计算他们的差异。
公式为: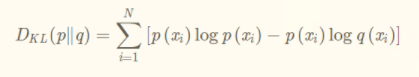
KL散度越小,表示P(x)和Q(x)越接近,所以可以通过反复训练,来使Q(x)逼近P(x),但KL散度有个特点,就是不对称,就是用P来你和Q和用Q来你和P的KL散度(相对熵)是不一样的,但是P和Q的距离是不变的。
那KL散度(相对熵)和交叉熵有什么联系呢?
我们通过对相对熵公式进行变形: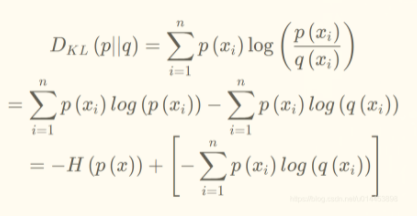
H(X)为之前的信息熵,后面那一坨其实就是交叉熵了,所以可以看到:**KL散度 = 交叉熵 - 信息熵**
所以交叉熵的公式如下: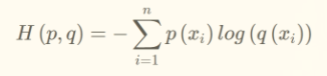
从信息熵的公式,我们知道,对于同一个数据集,其信息熵是不变的,所以信息熵可以看作一个常数,因此当KL散度最小时,也即是当交叉熵最小时。在多分类任务中,KL散度(相对熵)和交叉熵是等价的。
交叉熵的原理
交叉熵是用来衡量两个 概率分布 的距离(也可以叫差别)。[概率分布:即[0.1,0.5,0.2,0.1,0.1],每个类别的概率都在0~1,且加起来为1]。
若有两个概率分布p(x)和q(x),通过q来表示p的交叉熵为:(注意,p和q呼唤位置后,交叉熵是不同的)
$H ( p , q ) = - \sum p ( x ) \log q ( x )$
只要把p作为正确结果(如[0,0,0,1,0,0]),把q作为预测结果(如[0.1,0.1,0.4,0.1,0.2,0.1]),就可以得到两个概率分布的交叉熵了,交叉熵值越低,表示两个概率分布越靠近。
交叉熵计算实例:
假设有一个三分类问题,某个样例的正确答案是(1,0,0),某个模型经过softmax回归之后的预测答案是(0.5,0.4,0.1),那么他们的交叉熵为: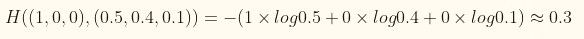
如果另一个模型的预测概率分布为(0.8,0.1,0.1),则这个预测与真实的交叉熵为: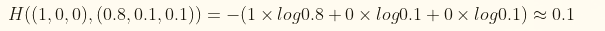
由于0.1小于0.3,所以第二个预测结果要由于第一个。
使用交叉熵的背景
通过神经网络解决分类问题时,一般会设置k个输出点,k代表类别的个数,如下图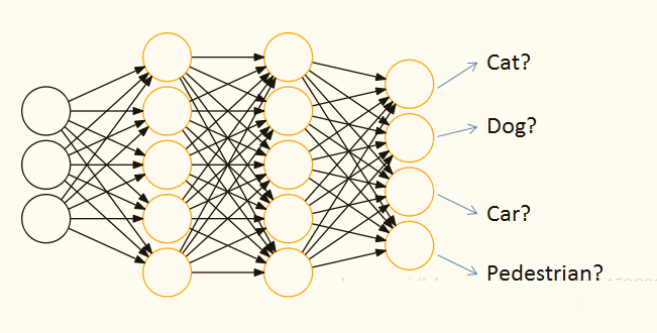
每个输出结点,都会输出该结点对应类别的得分,如[cat,dog,car,pedestrian] 为[44,10,22,5]
但是输出结点输出的是得分,而不是概率分布,那么就没有办法用交叉熵来衡量预测结果和真确结果了,那怎么办呢,**解决方法是在输出结果后接一层 softmax,softmax的作用就是把输出得分换算为概率分布**。












